A special feature of electric vehicles is their ability when braking or coming to a stop to use the momentum of the vehicle to turn the motor like a generator and put energy from the motor back into the battery.
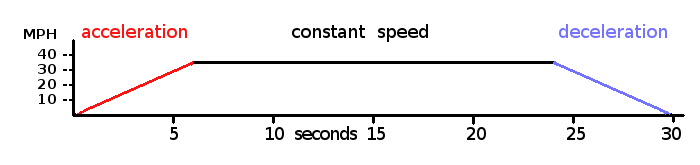
The momentum of a vehicle is its mass or "weight" times its velocity or "speed." In scenarios involving wholly straight line motion (as in the models here) the terms velocity and speed are interchangeable. The term "weight" is the force a mass exerts in a gravitational field. It is necessary to use mass in calculations of momentum, but that can be found from the weight. Since the mass of a vehicle doesn't change (It is usually illegal to through things out the windows.), the graph of momentum has the same shape as the graph of the velocity. The graphs here show straight line velocity (with no specific direction), or here speed, and the momentum is directly proportional. Using a mass unit equal to "1 car mass" makes the graph of momentum here identical to the graph of speed × 1 (car mass). A mass traveling at a high speed has a lot of momentum. A mass traveling at a slower speed has less.
Notice that the momentum only increases while the vehicle is accelerating to its cruising speed. While traveling at a constant speed the momentum is also constant. That is, the momentum at 24 seconds is the same as it was at 6 seconds.
Although electric vehicles can convert some of the energy of momentum back into electric power, that does not include the energy required to hold momentum constant. In a scenario with no friction at all it would take no energy to hold momentum constant. That is the reason highway mileage for gasoline powered vehicles is so much better. It is only necessary to overcome the friction of the air and metal parts inside the vehicle, however well oiled. That is a very significant amount of friction though for any vehicle and requires a significant amount of energy, none of which is adding anything to the momentum and therefore cannot be recovered from momentum.
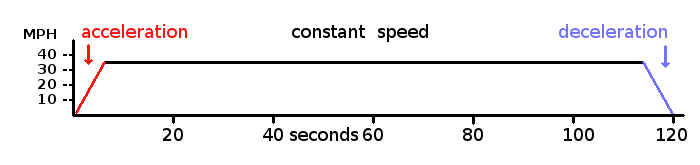
The first graph represents a jaunt of about one quarter mile at about 35 mph. That takes about 30 seconds. The second graph represents a journey of about one mile at 35 mph. That takes about 120 seconds or 2 minutes. Notice that this time the momentum at 114 seconds! is still the same as it was at 6 seconds. The point here is that as the length of a journey increases the percentage of energy that might be recovered from momentum significantly decreases.
When traveling on highways or anywhere the distance from start to stop is five miles or more the ability of an electric vehicle to recover energy from momentum becomes entirely irrelevant. Taking longer to accelerate in order to shorten the constant speed section of the graph will do little good since the momentum will still be the same as it was at 6 seconds. The overall average speed will be less so that might save something, just as driving slower might. The thing to remember though is that even during acceleration those forces of friction found at constant speed are still approximately the same there.
Another thing an electric vehicle can do is use no energy at all to stand still. Gasoline powered vehicles usually have to keep the engine on at an "idle." In the sort of traffic conditions where electric cars actually begin to show advantages over gasoline powered vehicles, bicycles show advantages over electric cars. The irony there is that the more crowded the road, the less welcome are bicycles. In a future where energy becomes scarce there could be more accommodations for bicycles.
In the previous article it was explained that increasing the number of electric vehicles does nothing to reduce fossil fuel consumption. The only practical way to reduce fossil fuel consumption rates is to construct new facilities for solar, wind, and hydroelectric power production where it is possible. Where that is possible can be a big problem. Solar and wind power generation can take much space, and still have meager results. There is a limit to how much energy a river can produce. Long stretches of many rivers are through virtually flat areas. Controlling flooding is a problem. Many rivers have dry seasons. Even high powered stations like Blenheim Gilboa have small service areas, and that station has the advantage of being in the mountains. Of course the Grand Coulee station has 6 times the capacity of Blenheim Gilboa, but those best spots are usually already taken.